











Дознај повеќе

Дознај повеќе

Дознај повеќе
Дознај повеќе





Пробниот час е бесплатен! Дознајте повеќе за ценовникот и начинот на плаќање.
Пораката се испраќа...

Скратена постапка за проверување дали некој број се дели со друг пришто резултатот би бил цел број, без да го извршиме делењето.

Само дел од фасцинантните математики длабоко вкоренети во историската игра шах.
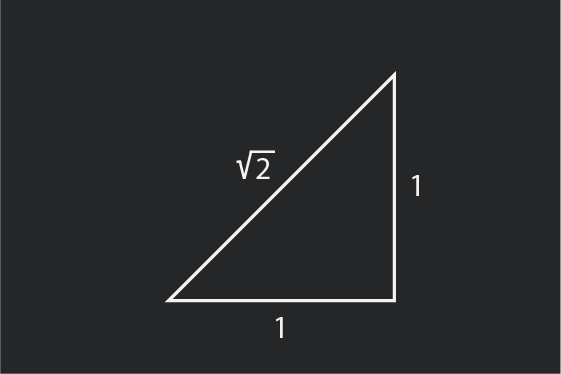
Доказ дека квадратниот корен на бројот 2 е број чиј децимален дел е бесконечен и не се повторува.
